CSC165: SLOG - Induction, Course Notes 56-58 --------------[ Week 8 ]

Hurray! Test #2 seem to have turned out well, with a 73% average! The majority of the class should be happy. It's moments like these that reminds me of high school, too bad not all moments in university are going to be like this one... Why must life be so cruel~! ...

Anyways... as the title shows, induction was touched upon this week, and in addition to the descriptive definition of induction, that was provided on tuesday, we were given a symbolic definition as well (shown below):

(P(k) ^ ( 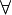n - {0, ... , k-1}, P(n) 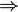P(n+1))) 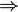( 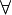n - {0, ... , k-1}, P(n))

This symbolic definition was interesting to me in the sense that it used a "-" to exclude a set and soon after the class reacted to this as well. This led to a small preference poll on Danny's selected use of exclusion, I voted "\", unfortunately I was out voted and a minority (darn you democratic system!). Anyways, after this we proved the following:

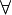( n , 3^n > n^3), which was adjusted to (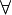 n - {0, 1, 2, 3}, P(n) 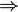P(n+1))

where P(n): 3^n > n^3

This proof was very interesting because it really added to the bridge that connected MAT137 to CSC165, not to say that any of the other proofs did not. It was just that this one seemed to stand above all. This reminds me that I should state how I've also been applying these symbolic notations to the MAT137 theorems presented in class, and that it has really helped in my understandings of the theorems. This also includes the fact that it shortened the definition dramatically. I now understand why many say this course should have been taught in the first semester and not in the second.

The last topic provided on Friday was the Fibonacci Sequence, which was a bit confusing since, I didn't understand how the following was derived:

k
F(i) = F (k+2) - 1
i=0

I plan to get help from a friend or the CS Help Center this upcoming week, other than that this week went pretty good! [Been a while since I left a test happy :) ]