Finally, the last week has come week 12! And with it the last test!, Test #3 on Big-Oh and Big-Omega. I'm extremely glad that floating point numbers were not placed within this test, since as I have spoken in my previous post, of my confusion of floating point numbers! Overall, I believe I did fairly well on this test, though I feel a bit uneasy of my conclusions, since I wasn't exactly too sure in some cases as to whether I have fully concluded in respect to my introductions of each proof. Nevertheless, I can't complain, since I felt this test in sum wasn't terrible, mainly because I worked hard to study and complete assignment #3.
On the last day we spoke of condition numbers and how to derive it and to our surprise, the process of finding the formula for conditional numbers leads us to the derivative of the function. This derivative is multiplied by abs( x/ f(x)), which was taken out during the process of deriving the formula for the conditional number. Using this knowledge in action shows the conditional number of x^5 is... well as said before take the derivative and multiply that with abs(x/ the function itself (x^5) ), returning 5, I'm not exactly sure but I believe since the conditional number is a ratio of the relative error, then the smaller it is the more stability it should have. However, in the case of another function being made from this kind of process (ex/ |x*tanx|) I'm quite confused...
The next important point of conditional numbers are that:
"A well conditional number is necessary for stability, but it is not sufficient!"
Now, the question is what does stability mean in that sense? Well, an example of a unstable algorithm or expression is, 100 + 0.1 + 0.1, which will round down to 100 if the 0.1s aren't added first, as well as 11.1156 - 11.1264, rounding down to 0. [Catastrophic Cancellation!]. The quadratic formula was spoken upon next and then a method to approximate functions. The approximation of functions led us to the Taylor Polynomial/Series, and an island where all we had was the sand and a stick to calculate e^x.
In the last slide, we found we can break up the approximation and the function into two parts, to account for the source of error by using the triangle inequality, |g(x') - f(x)|, where g(x') is the approximated function of f applied to an approximate x value x'.
This about wraps up CSC165... and I have to say, I never expected this course to be so amazingly interesting, especially when I first heard it was a proof/logic filled course. Surprisingly I think I found this course more interesting than 148, though my final decision is yet to be decided.
Nevertheless, I had an excellent time in CSC165, thanks Danny! I hope to have you as a professor for another course in the later years, you're an awesome prof!
The End.
Monday, March 29, 2010
CSC165: SLOG - Lies Computers Tell Us --------------[ Week 11 ]--------------
Before I begin my post on Week 11, I just wanted to state that the video Danny created was very informative, anybody reading this that doesn't understand Big-Oh MUST watch it, it takes you through the entire process of a big-Oh proof and should be watched repetitively until the Big-Oh concept sinks in! The link is below:
"http://www.cdf.toronto.edu/~heap/165/Movies/bigOh.html"
At any rate, the topic spoken about this week was extremely confusing to me, being of floating-point numbers. At first I understood what Danny meant with base 2, # of digits allowed, exponents running from [-2, 3], etc. However, when the talk of radix point, adjacent numbers and the number list came, I became surprisingly lost in every possible way! From the point of the number list and onwards I hadn't much of any clue of what was being taught, except for the relative error formula. I understand that I must seek help immediately and I plan to do so with the last office hour placed in our final week (Week 12).
"http://www.cdf.toronto.edu/~heap/165/Movies/bigOh.html"
At any rate, the topic spoken about this week was extremely confusing to me, being of floating-point numbers. At first I understood what Danny meant with base 2, # of digits allowed, exponents running from [-2, 3], etc. However, when the talk of radix point, adjacent numbers and the number list came, I became surprisingly lost in every possible way! From the point of the number list and onwards I hadn't much of any clue of what was being taught, except for the relative error formula. I understand that I must seek help immediately and I plan to do so with the last office hour placed in our final week (Week 12).
Monday, March 22, 2010
CSC165: SLOG - More Asymptotics ---------------[ Week 10 ]--------------
The awesome sounding "big-Omega!" was introduced, and with a somewhat similar name came a relatively similar definition. As big-O was focused on a function being bounded above by another function, big-Omega focuses on a function being the upper bound of another function. The two definitions are entirely the same except for the inequality signs. Where big-Oh holds f(n) <= cg(n), and big-Omega holds f(n) >= cg(n). It also followed that a function can be bounded above and below by the same function ( f belongs to O(G) ^ f belongs to Omega(g) ). If this this concept is true, we represent it as "Big-Pheta", where c1*g(n) <= f(n) <= c2*g(n). The proof of general statements about two functions followed, as well as a big-O implying a big-Omega (f 
O(g) => g Omega(f)).
The proof of... f O(g) => f*f O(g*g), was shown on Wednesday as well as,
(f O(h) ^ g O(h)) => (f + g) O(h) and the disproof of f O(g) => f O(g*g)
On Friday we discussed patterns of linear search and derived formulas for the number of steps a linear search takes. We also discussed which of the three speed: best, worst, and average... was most important. In the end, the worst case proved itself to be the most important speed to which we care about since we are able to guarantee a lower bound, as in this search will be in the worst case ______, rather than saying the average and best speed (which is less valuable). And with all of this, we then finally proved that a certain sort was in the worst case bounded above by n^2. I believe this was the most confusing part of this week, in the fact that we didn't use a formula given but a formula we had to derive from the python code.
Nevertheless, this week was quite packed and was a bit hard to keep up with, I plan to go to the CSSU help center to go over these notes carefully, just to make sure I understand these new concepts.
O(g) => g Omega(f)).The proof of... f
O(g) => f*f O(g*g), was shown on Wednesday as well as,(f
O(h) ^ g O(h)) => (f + g) O(h) and the disproof of f O(g) => f O(g*g)On Friday we discussed patterns of linear search and derived formulas for the number of steps a linear search takes. We also discussed which of the three speed: best, worst, and average... was most important. In the end, the worst case proved itself to be the most important speed to which we care about since we are able to guarantee a lower bound, as in this search will be in the worst case ______, rather than saying the average and best speed (which is less valuable). And with all of this, we then finally proved that a certain sort was in the worst case bounded above by n^2. I believe this was the most confusing part of this week, in the fact that we didn't use a formula given but a formula we had to derive from the python code.
Nevertheless, this week was quite packed and was a bit hard to keep up with, I plan to go to the CSSU help center to go over these notes carefully, just to make sure I understand these new concepts.
Monday, March 15, 2010
CSC165: SLOG - Asymptotics [Big-Oh] ---------Course Notes Chapter 5 ---------------------[ Week 9 ]
This week's lectures opened up with sorting strategies, introducing insertion & selection sort. To properly introduce these algorithms Danny opened up by using these methods to sort a hand of cards. I must say that the moment he asked the class, what type of sorting method each of one us prefers to use, I had an overwhelming urge to shout out "BUBBLE-SORT!!", unfortunately I didn't do so, though it would've been an interesting topic to speak upon.
Next topic was the big-Oh definition, not too much to say here, simply that the definition states, in terms of limits, if n approaches infinity, the function f(n) will be no bigger than c(g(n)), once the appropriate c is found. Big-Oh is quite straight forward. After the introduction of this definition Danny followed with a proof of a function being no bigger than another function or in other words the first function is bounded above by the second. I compared the proof done with the evening section and the suggestion made for the afternoon section was much more complicated, I see the reason why Danny suggested everyone to take a look at the evening section and it's to show that there is, I suppose in my personal understandings, an easier/simpler method, and that we should strive for the simplest solution.
Afterward, the disproof followed and soon l'Hopital was introduced to aid in the explanation of the disproof. I wasn't exactly too sure, but I believe the purpose of l'Hopital was to show that the property (2^n)/(n^2) works to infinity and by using l'Hopital to show this, it works that for all n that property is > c (where c can be any real number[+]). My question is, if this is true, does that mean we have to show l'Hopital for each proof? Or was that just an in depth explanation to why this disproof is true?
Nevertheless, that was Week 9!, only 3 more weeks to go... :( university years sure pass by quickly...
Next topic was the big-Oh definition, not too much to say here, simply that the definition states, in terms of limits, if n approaches infinity, the function f(n) will be no bigger than c(g(n)), once the appropriate c is found. Big-Oh is quite straight forward. After the introduction of this definition Danny followed with a proof of a function being no bigger than another function or in other words the first function is bounded above by the second. I compared the proof done with the evening section and the suggestion made for the afternoon section was much more complicated, I see the reason why Danny suggested everyone to take a look at the evening section and it's to show that there is, I suppose in my personal understandings, an easier/simpler method, and that we should strive for the simplest solution.
Afterward, the disproof followed and soon l'Hopital was introduced to aid in the explanation of the disproof. I wasn't exactly too sure, but I believe the purpose of l'Hopital was to show that the property (2^n)/(n^2) works to infinity and by using l'Hopital to show this, it works that for all n that property is > c (where c can be any real number[+]). My question is, if this is true, does that mean we have to show l'Hopital for each proof? Or was that just an in depth explanation to why this disproof is true?
Nevertheless, that was Week 9!, only 3 more weeks to go... :( university years sure pass by quickly...
Sunday, March 7, 2010
CSC165: SLOG - Induction, Course Notes 56-58 --------------[ Week 8 ]
Hurray! Test #2 seem to have turned out well, with a 73% average! The majority of the class should be happy. It's moments like these that reminds me of high school, too bad not all moments in university are going to be like this one... Why must life be so cruel~! ...
Anyways... as the title shows, induction was touched upon this week, and in addition to the descriptive definition of induction, that was provided on tuesday, we were given a symbolic definition as well (shown below):
(P(k) ^ (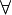
n 
- {0, ... , k-1}, P(n)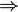 
P(n+1))) 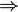( 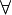n - {0, ... , k-1}, P(n))
This symbolic definition was interesting to me in the sense that it used a "-" to exclude a set and soon after the class reacted to this as well. This led to a small preference poll on Danny's selected use of exclusion, I voted "\", unfortunately I was out voted and a minority (darn you democratic system!). Anyways, after this we proved the following:
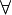( n , 3^n > n^3), which was adjusted to (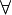 n - {0, 1, 2, 3}, P(n) 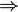P(n+1))
where P(n): 3^n > n^3
This proof was very interesting because it really added to the bridge that connected MAT137 to CSC165, not to say that any of the other proofs did not. It was just that this one seemed to stand above all. This reminds me that I should state how I've also been applying these symbolic notations to the MAT137 theorems presented in class, and that it has really helped in my understandings of the theorems. This also includes the fact that it shortened the definition dramatically. I now understand why many say this course should have been taught in the first semester and not in the second.
The last topic provided on Friday was the Fibonacci Sequence, which was a bit confusing since, I didn't understand how the following was derived:
k
F(i) = F (k+2) - 1
i=0
I plan to get help from a friend or the CS Help Center this upcoming week, other than that this week went pretty good! [Been a while since I left a test happy :) ]
Anyways... as the title shows, induction was touched upon this week, and in addition to the descriptive definition of induction, that was provided on tuesday, we were given a symbolic definition as well (shown below):
(P(k) ^ (
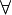n - {0, ... , k-1}, P(n) 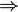P(n+1))) 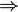( 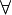n - {0, ... , k-1}, P(n))This symbolic definition was interesting to me in the sense that it used a "-" to exclude a set and soon after the class reacted to this as well. This led to a small preference poll on Danny's selected use of exclusion, I voted "\", unfortunately I was out voted and a minority (darn you democratic system!). Anyways, after this we proved the following:
(
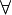n , 3^n > n^3), which was adjusted to (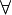 n - {0, 1, 2, 3}, P(n) 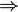P(n+1))where P(n): 3^n > n^3
This proof was very interesting because it really added to the bridge that connected MAT137 to CSC165, not to say that any of the other proofs did not. It was just that this one seemed to stand above all. This reminds me that I should state how I've also been applying these symbolic notations to the MAT137 theorems presented in class, and that it has really helped in my understandings of the theorems. This also includes the fact that it shortened the definition dramatically. I now understand why many say this course should have been taught in the first semester and not in the second.
The last topic provided on Friday was the Fibonacci Sequence, which was a bit confusing since, I didn't understand how the following was derived:
k
F(i) = F (k+2) - 1i=0
I plan to get help from a friend or the CS Help Center this upcoming week, other than that this week went pretty good! [Been a while since I left a test happy :) ]
Wednesday, March 3, 2010
PROBLEM SOLVING: Paper "Folding"
----------------------------------------------------------------------------------
Understanding The Problem:
----------------------------------------------------------------------------------
At first glance, I assumed this was going to be easy, since it's titled "Folding", like honestly how hard could it possibly be right? It's "Folding"!... so much for that assumption...
The problem is to take a strip of paper and fold it several times, while analyzing the pattern of down(s) and up(s) that occur upon each fold. This is restricted to a consistent orientation. The objective of this problem is to come up with an output being a formula/method in predicting the sequences of up(s) and down(s) given a number of folds.
----------------------------------------------------------------------------------
Devise A Plan:
----------------------------------------------------------------------------------
Nevertheless, after reading the handout I thought it would be a wise move to follow the instructions provided on the handout And so, I devised the following plan.
[Step 1] Begin folding strips to see what occurs and understand what is meant by the problem practically.
[Step 2] Restart with a fresh strip and begin recording the number of ups and downs to see if there is a numerical pattern
[Step 3] If numerical pattern does not seem to exist or no method/formula can be concluded, restart from the beginning and record the actual pattern displayed between each folding. (1-5 folds should be sufficient)
[Step 4] Analyze the illustrated pattern from step 3
[Step 5] If no eureka occurs, go to office hours :)
----------------------------------------------------------------------------------
Carry Out The Plan & Look Back:
----------------------------------------------------------------------------------
[During Step 1] I was instantly intrigued by this problem, it presented itself to be much more difficult than I had realized initially. No pattern seemed to present itself during this stage of mass fiddling.
[During Step 2] After recording the number of up(s) and down(s), which was extremely terrible at fold 4 and 5. I managed to conjure up a pattern, being that the # of down(s) increases by a multiplication of 2 each fold (this made me feel pretty good, since it was some progress), initially starting a 1 and that the # of up(s) held the following increasing patterns 0, 1, 2, 4, 8... initially starting at 0. I soon realized that this wasn't much of any help at all and proceeded with step 3.
[During Step 3] Recording was definitely annoying at fold 4 and 5 once again. It was like reading the cheat sheet I made for test 1... (....Okay, no not really, but it was definitely tedious). The reason was that it became much more difficult to read as the up(s) and down(s) were becoming less defined upon fold 5. Nevertheless as planned, I had proceeded to analyze the data. It took approximately 3 minutes before I had realized that the previous pattern of up(s) & down(s) were preserved upon the right of the next pattern to follow.
Ex/ ↑↓
1-Fold: ↓
2-Fold: ↑↓↓
3-Fold: ↑↑↓↓↑↓↓
4-Fold: ↑↑↓↑↑↓↓↓↑↑↓↓↑↓↓
5-Fold: ↑↑↓↑↑↓↓↑↑↑↓↓↑↓↓↓↑↑↓↑↑↓↓↓↑↑↓↓↑↓↓
This gave me a strong glimpse of hope that I may be able to solve this problem soon!... Unfortunately about an hour had passed and I still didn't notice any other patterns besides that the extremes were of opposite directions consistently for each fold. It wasn't til 10 minutes after this that I had found a mirrored pattern marching to the center of each fold and within the center lied the FIRST FOLD!. This was the eureka moment I had been waiting for! It felt tremendously awesome
Illustration:
1-Fold: ..................................↓
2-Fold: ...............................↑ ↓ ↓
3-Fold: .......................... ↑↑↓ ↓ ↑↓↓
4-Fold: ..................↑↑↓↑↑↓↓ ↓ ↑↑↓↓↑↓↓
5-Fold: ↑↑↓↑↑↓↓↑↑↑↓↓↑↓↓ ↓ ↑↑↓↑↑↓↓↓↑↑↓↓↑↓↓
Hence, the solution to predicting the sequence of up(s) and down(s) for the n-th fold is to know the previous sequence and maintain a mirrored version of that previous sequence on the left and right of the first orientated fold (as shown above).
However, this is all assumed relatively like induction, as it works for 1, 2, 3, 4, 5 folds as the base case, it may not work for the 6th. Then comes the reasoning behind the mirrored series' appearance, which is the folding motion of say... the left end to the right end (or the original orientation used). This flips the previous folds held within the left section, but maintains the center being the 1-Fold, this implies that the (n + 1)-th fold will maintain the same structure/pattern.
Ex/ ____o____ ........................../
.........................................../ ....↓
........................................./
.......................................o____________
Therefore, Q.E.D :) !
----------------------------------------------------------------------------------
Acknowledge When, And How, You're Stuck:
----------------------------------------------------------------------------------
[During Step 2]: This step was a mistake since I was working with the # of up(s) and down(s), not the sequence... unfortunately I didn't realize this until the end.
[During Step 3]: My 2nd mistake I believe was within that approximately 1 hr duration period, which I was stuck. What I should have done was focus on what was occurring to the folds that had already been made during the next fold to come. This probably could have led me to the final answer more quickly, but instead I focused too much on deriving a pattern within the illustrated example.
Understanding The Problem:
----------------------------------------------------------------------------------
At first glance, I assumed this was going to be easy, since it's titled "Folding", like honestly how hard could it possibly be right? It's "Folding"!... so much for that assumption...
The problem is to take a strip of paper and fold it several times, while analyzing the pattern of down(s) and up(s) that occur upon each fold. This is restricted to a consistent orientation. The objective of this problem is to come up with an output being a formula/method in predicting the sequences of up(s) and down(s) given a number of folds.
----------------------------------------------------------------------------------
Devise A Plan:
----------------------------------------------------------------------------------
Nevertheless, after reading the handout I thought it would be a wise move to follow the instructions provided on the handout And so, I devised the following plan.
[Step 1] Begin folding strips to see what occurs and understand what is meant by the problem practically.
[Step 2] Restart with a fresh strip and begin recording the number of ups and downs to see if there is a numerical pattern
[Step 3] If numerical pattern does not seem to exist or no method/formula can be concluded, restart from the beginning and record the actual pattern displayed between each folding. (1-5 folds should be sufficient)
[Step 4] Analyze the illustrated pattern from step 3
[Step 5] If no eureka occurs, go to office hours :)
----------------------------------------------------------------------------------
Carry Out The Plan & Look Back:
----------------------------------------------------------------------------------
[During Step 1] I was instantly intrigued by this problem, it presented itself to be much more difficult than I had realized initially. No pattern seemed to present itself during this stage of mass fiddling.
[During Step 2] After recording the number of up(s) and down(s), which was extremely terrible at fold 4 and 5. I managed to conjure up a pattern, being that the # of down(s) increases by a multiplication of 2 each fold (this made me feel pretty good, since it was some progress), initially starting a 1 and that the # of up(s) held the following increasing patterns 0, 1, 2, 4, 8... initially starting at 0. I soon realized that this wasn't much of any help at all and proceeded with step 3.
[During Step 3] Recording was definitely annoying at fold 4 and 5 once again. It was like reading the cheat sheet I made for test 1... (....Okay, no not really, but it was definitely tedious). The reason was that it became much more difficult to read as the up(s) and down(s) were becoming less defined upon fold 5. Nevertheless as planned, I had proceeded to analyze the data. It took approximately 3 minutes before I had realized that the previous pattern of up(s) & down(s) were preserved upon the right of the next pattern to follow.
Ex/ ↑↓
1-Fold: ↓
2-Fold: ↑↓↓
3-Fold: ↑↑↓↓↑↓↓
4-Fold: ↑↑↓↑↑↓↓↓↑↑↓↓↑↓↓
5-Fold: ↑↑↓↑↑↓↓↑↑↑↓↓↑↓↓↓↑↑↓↑↑↓↓↓↑↑↓↓↑↓↓
This gave me a strong glimpse of hope that I may be able to solve this problem soon!... Unfortunately about an hour had passed and I still didn't notice any other patterns besides that the extremes were of opposite directions consistently for each fold. It wasn't til 10 minutes after this that I had found a mirrored pattern marching to the center of each fold and within the center lied the FIRST FOLD!. This was the eureka moment I had been waiting for! It felt tremendously awesome
Illustration:
1-Fold: ..................................↓
2-Fold: ...............................↑ ↓ ↓
3-Fold: .......................... ↑↑↓ ↓ ↑↓↓
4-Fold: ..................↑↑↓↑↑↓↓ ↓ ↑↑↓↓↑↓↓
5-Fold: ↑↑↓↑↑↓↓↑↑↑↓↓↑↓↓ ↓ ↑↑↓↑↑↓↓↓↑↑↓↓↑↓↓
Hence, the solution to predicting the sequence of up(s) and down(s) for the n-th fold is to know the previous sequence and maintain a mirrored version of that previous sequence on the left and right of the first orientated fold (as shown above).
However, this is all assumed relatively like induction, as it works for 1, 2, 3, 4, 5 folds as the base case, it may not work for the 6th. Then comes the reasoning behind the mirrored series' appearance, which is the folding motion of say... the left end to the right end (or the original orientation used). This flips the previous folds held within the left section, but maintains the center being the 1-Fold, this implies that the (n + 1)-th fold will maintain the same structure/pattern.
Ex/ ____o____ ........................../
.........................................../ ....↓
........................................./
.......................................o____________
Therefore, Q.E.D :) !
----------------------------------------------------------------------------------
Acknowledge When, And How, You're Stuck:
----------------------------------------------------------------------------------
[During Step 2]: This step was a mistake since I was working with the # of up(s) and down(s), not the sequence... unfortunately I didn't realize this until the end.
[During Step 3]: My 2nd mistake I believe was within that approximately 1 hr duration period, which I was stuck. What I should have done was focus on what was occurring to the folds that had already been made during the next fold to come. This probably could have led me to the final answer more quickly, but instead I focused too much on deriving a pattern within the illustrated example.
Monday, March 1, 2010
CSC165: SLOG - Epsilon-Delta Proofs and More Proof Techniques --------------[ Week 7 ]
Week 7, it's hard to believe that 7 weeks has passed since this course began, it felt so short. This week started with Danny introducing us to all the computer science aid, being the CSC Help Center which most of the students are very unaware of, I'm sure, following with office hours and TA office hours.
The materials that were covered afterward was none other than the infamous epsilon delta proofs, at first I was very frightened, although I "had" mastered the material in proving in MAT137, it was through weeks of struggle. Even then, after understanding all of the meaning of finding the upper and lower bound, it took about another entire week before it clicked. Unfortunately, on the day of Danny teaching this topic, in the form of a structured proof, I was nearly clueless on how the delta was found/chosen, since I had forgotten most of it. However, it soon made sense after I had reviewed the proof at home and a bit of MAT137. Though I could not say I was as confident as I was on the first MAT137 test.
Wednesday, unfortunately was terrible, not because of Danny's teaching, but because of the CSC148 test, that came out with an overall 50% average. I was practically mentally damaged after that traumatizing event and was not able to focus too well on what was being taught. However, after going home and working up my self-esteem I reviewed the material and understood it. This was a very unfortunate day in my life as I have never been placed in such a position in realizing that the most I could possibly get on a test was approx. 40% and with this... I can honestly say... Welcome to University... (*Sighh*).
Friday was a bit of a freebie and by freebie I mean a relaxing lecture. We followed up on a new possible problem-solving question for the SLOG titled biological sequences. Although I understood the algorithm everyone was speaking of, I couldn't see myself being able to code such a difficult task, at most I could probably describe what everyone was getting at in relative terms.
In the end of the week, I couldn't say it was an alright or amazing week because of CSC148, but everything went quite well for CSC165, which I am very glad for.
The materials that were covered afterward was none other than the infamous epsilon delta proofs, at first I was very frightened, although I "had" mastered the material in proving in MAT137, it was through weeks of struggle. Even then, after understanding all of the meaning of finding the upper and lower bound, it took about another entire week before it clicked. Unfortunately, on the day of Danny teaching this topic, in the form of a structured proof, I was nearly clueless on how the delta was found/chosen, since I had forgotten most of it. However, it soon made sense after I had reviewed the proof at home and a bit of MAT137. Though I could not say I was as confident as I was on the first MAT137 test.
Wednesday, unfortunately was terrible, not because of Danny's teaching, but because of the CSC148 test, that came out with an overall 50% average. I was practically mentally damaged after that traumatizing event and was not able to focus too well on what was being taught. However, after going home and working up my self-esteem I reviewed the material and understood it. This was a very unfortunate day in my life as I have never been placed in such a position in realizing that the most I could possibly get on a test was approx. 40% and with this... I can honestly say... Welcome to University... (*Sighh*).
Friday was a bit of a freebie and by freebie I mean a relaxing lecture. We followed up on a new possible problem-solving question for the SLOG titled biological sequences. Although I understood the algorithm everyone was speaking of, I couldn't see myself being able to code such a difficult task, at most I could probably describe what everyone was getting at in relative terms.
In the end of the week, I couldn't say it was an alright or amazing week because of CSC148, but everything went quite well for CSC165, which I am very glad for.
Subscribe to:
Posts (Atom)
